| Главная » Статьи » Геометрия |
Начертательная геометрия ( да да та самая начерталка, которая является головной болью многих студентов) – это прекрасный пример Евклидовой геометрии. Но является ли она единственно возможной, и если нет то, каково значение этих «других» геометрий в современном мире. На данный момент создано три «основных геометрии»: Евклидова геометрия, Геометрия Римана, Геометрия Лобачевского (гиперболическая геометрия). Но в чем их отличие друг от друга? Для начала определимся, что такое геометрия — это раздел математики, изучающий пространственные структуры, отношения и их обобщения. Итак, в чем же различие этих трех столпов современной
геометрии? Евклидова геометрия (или элементарная геометрия) — геометрическая теория, основанная на системе аксиом, впервые изложенной в «Началах» Евклида (III век до н. э.), для нее характерна «работа с пространством», имеющим нулевую кривизну (см. рис 1). Евклидова аксиома о параллельных гласит: Через точку, не
лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой
в одной плоскости и не пересекающей её. Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского. В геометрии Лобачевского, вместо неё принимается следующая
аксиома: Через точку, не лежащую на данной прямой, проходят по крайней мере две
прямые, лежащие с данной прямой в одной плоскости и не пересекающие её (см. рис
1) С современной точки зрения, геометрия Лобачевского представляет собой
геометрию пространства постоянной отрицательной кривизны. Представление о ней
можно получить, изучая модели плоскости Лобачевского, такие как модель Клейна,
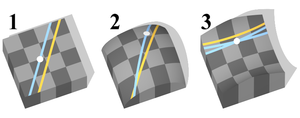
модели Пуанкаре и др. В геометрии Римана прямая определяется двумя точками, плоскость — тремя, две плоскости пересекаются по прямой и т.д., но через данную точку нельзя провести к прямой ни одной параллельной (см. рис. 1). В геометрии Римана, как и в сферической геометрии, справедливо утверждение: сумма углов треугольника больше двух прямых. Геометрия Римана реализуется на поверхностях с постоянной положительной гауссовой кривизной, т.е. на сферах.
(1) евклидова геометрия; (2) геометрия Римана; (3) геометрия Лобачевского Итак, геометрия Евклида реализуется на поверхностях с постоянной нулевой гауссовой кривизной, Лобачевского — с постоянной отрицательной, геометрия Римана реализуется на поверхностях с постоянной положительной гауссовой кривизной, т.е. на сферах. Но что же из этого вытекает, какое практическое значение имеет это «множество геометрий»? А вот какое: в XX в. было обнаружено, что геометрия Лобачевского не только имеет важное значение для абстрактной математики, как одна из возможных геометрий, но и непосредственно связана с приложениями математики к физике. Оказалось, что взаимосвязь пространства и времени, открытая в работах X. Лоренца, А. Пуанкаре, А. Эйнштейна, и описываемая в рамках специальной теории относительности, имеет непосредственное отношение к геометрии Лобачевского. Например, в расчетах современных синхрофазотронов используются формулы геометрии Лобачевского. Риманова геометрия служит фундаментом общей эйнштейновской теории
относительности. Геометрия Лобачевского нашла свои приложения в современной
физике, прежде всего в теории относительности, квантовой физике, теории
суперструн. То есть, неевклидовы геометрии имеют большое практическое
значение в фундаментальной науке, изучающей структуру вселенной (ее развитие и
этапы формирования), а также свойства отдельных «кусков» пространства, свойства
частиц и т.д. Но значит ли это, что эти геометрии совершенно бесполезны для не
посвященного в таинства современной науки? Конечно, нет! Просто следствия
многих фундаментальных открытий не так скоро доходят до уровня обычного обывателя. Вспомнить хотя
бы исследование мельчайших атомных частиц:
десятилетия ушли на изучение взаимодействий внутри атома, годы на внедрение
открытий в жизнь. И что мы имеем в итоге? В итоге мы освоили новые виды энергии
(АЭС), ядерное оружие. Открытие новых материалов позволило превратить
компьютерные комплексы, величиной с целую комнату, в небольшие портативные
система (ноутбуки). Таким образом, помогая изучать глубинные основы мироздания,
новые формы взаимодействия пространства-материи, геометрия открывает совершенно
новый, принципиально более высокий уровень развитие человечества, позволяющий
взглянуть внутрь стольких тайн, ранее закрытых для человечества! | |
| Просмотров: 3984 | Рейтинг: 4.0/2 |
| Всего комментариев: 0 | |